Zengin Öğrenme Ortamları Tasarlamak Nedir, Ne Değildir?

Yazar: Dilan Özdemir, Matematik Öğretmeni

Zengin öğrenme ortamları denilince yoğun teknoloji kullanımı, her şeyi “eğlenceli” oyunlar haline getirmek, kartonlara boğulmuş sınıflar geliyordu aklıma. Derslerimde oyunlara yer vererek “eğlenceli ve öğretici” bir matematik dersi yaptığımı sanıyordum. Evet, matematik dersinde su dolu balonlar patlatmak, birbirini kovalamak, kahkahalar atmak, bahçeye çıkmak şüphesiz eğlenceliydi. Fakat öğrenme-öğretme süreçlerini kapsamayan, yani özünde istenilen bilgi ve beceriyi kazandırma amacına hizmet etmeyen, bu oyunlar kesinlikle öğretici değildi. Ta ki geçen dönem Matematik Öğretimi Topluluğu ile birlikte TİMSS video çalışmasının(1) “açılar” konusunun yer aldığı Japon matematik dersini izleyene kadar fark edememiştim bunu. Bu dersten öğrendiklerimi sınıfıma nasıl yansıtmaya çalıştım, nereye kadar gidebildim, aklımda hangi sorular belirdi, neler deneyimledim bunların hepsinden tek tek bahsedeceğim. Fakat öncesinde bu Japon dersinde neler oluyor, sizlere bahsetmek istiyorum. Hatta yazının devamına geçmeden önce bahsettiğim bu dersi gözden geçirmenizi tavsiye ediyorum. Türkçe altyazı seçeneğini kullanarak izleyebilirsiniz.

Bir Japon Matematik Dersi

Dersin konusu, bizim Türkiye’de “paralel doğrular arasında bükülmüş doğruların oluşturduğu açılar” olarak bildiğimiz 7. sınıf matematik konusu. Öğretmen dersin başında bir önceki derse atıfta bulunurken bir yandan da yeni ders için çalışma kağıtları dağıtıyor. Tahtaya aşağıdaki soruyu yazıyor ve öğrencilerin soru üzerinde çalışarak en kolay olduğunu düşündükleri yöntemle çözmelerini istiyor (Görsel 1).

Belirli bir süre bireysel olarak soru üzerinde uğraşan sınıf üç farklı çözüm yöntemi sunuyor.

Toplu Sınıf Çalışması: Üç öğrenci çözüm yöntemlerini paylaşıyor.

Öğretmen bu defa öğrencilerden paralel doğrular arasındaki büküm sayısında daha serbest davranarak kendi sorularını kendilerinin yaratmasını istiyor. Öğrenciler bireysel olarak sorular yarattıktan sonra gruplarına dağılıyorlar. Her grup üretilen sorular üzerinde tartışıp tahtaya yazmak üzere, çözümünden emin oldukları birer soruyu sınıfa sunuyor. Ve tahtaya öğrencilerin kendi ürettiği altı soru yazılıyor (Görsel 3).

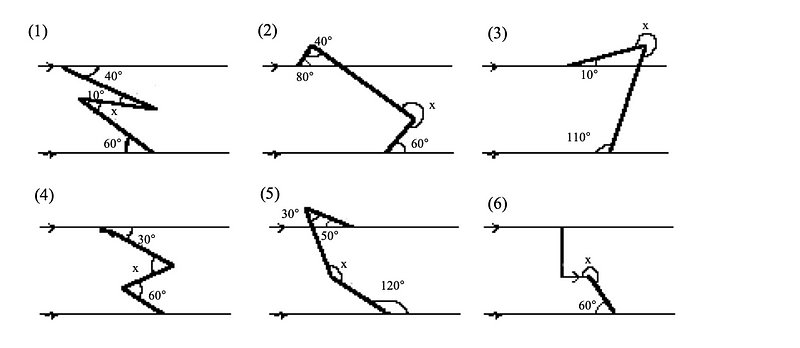
Tüm öğrenciler bu soruları çalışma kağıtlarına kopyalıyor. Soruları çözmek için en verimli/stratejik yöntemi seçerek uygulamaya çalışıyor ve bir ders sonlanıyor.(2)

Öğrendiklerimi Dersime Nasıl Yansıtmaya Çalıştım ?

İzlediğimiz bu dersleri Öğretim Açığı kitabı (Stigler ve Hiebert, 1999) eşliğinde yoğun bir şekilde tartışırken 7. sınıflarda açılar konusuna geçmiştim ve artık eski yöntemlerle derse giremeyeceğime karar verdim. İzlediklerimizden, tartıştıklarımızdan yola çıkarak bir ders planı tasarlamaya çalıştım. Öğretmenler odasının bir köşesinde yer alan ama kullanılmayan açıölçeri neden kullanmadığımızı düşündüm ve açıölçeri ders planıma dahil ettim. Öğrencilerden de sınıfa açıölçerle gelmelerini istedim. Derse başlarken tahtaya sadece şunları yazdım:

1. Birbirine paralel iki doğru çizelim.
2. İki paralel doğruyu kesen üçüncü bir doğru çizelim.
3. iki paralel ve bir kesen doğrunun oluşturduğu açıları açı ölçerle ölçelim.

Bir süre uğraştılar. Yönergeleri uygulayıp ortaya koydukları şekilleri tahtaya kopyaladım (Görsel 4).

Eğer, neredeyse tüm matematik öğretmenlerinin ilk ve tek tercihi olan şekilde çizimi önden ben yapsaydım, birinci çizim üzerinden tek yönlü bir ders işleyecektik. Matematik öğretmenleri olarak hepimizin muhtemel yaşadığı bir durum vardır; şekil değiştiği zaman öğrenciler gördükleri yeni şekil üzerine edindikleri bilgileri transfer becerisi gösteremezler. Bu becerinin neden gösterilmediği üzerine derinleşebiliriz elbette, derinleşilmeli de. Benim burda vurgulamak istediğim konu, henüz ilk adımda bile üretmeleri için fırsat verildiğinde öğrencilerin farklı olası durumları kendilerinin sunabiliyor olduğu.

Sonrasında öğrenciler kendilerinin ve arkadaşlarının çizdikleri şekillerin oluşturduğu açıları açı ölçerle ölçtüler. Birkaç ölçümden sonra “iki paralel doğru arasındaki karşılıklı açıların toplamının 180 derece”; kendi deyimleriyle “çapraz açıların” eşit; “komşu iki açının toplamının 180 derece” olduğunu fark edip, heyecanla arkadaşlarıyla ve benimle paylaşmaya başladılar. Aynı zamanda, “bir açıyı bulmanın diğer açıları bulmak için yeterli olduğunu” da fark edip dile getirdiler. Yöndeş, iç-ters, dış-ters açılar arasındaki ilişkiyi keşfetmede başarılı oldular.

“Öğretmenim anlayınca çok güzelmiş matematik, çok eğlenceli, ne çabuk geçti ders, keşke her konu böyle eğlenceli olsa.” gibi tepkiler verdiler. Öğrencinin ders araç gereçlerini yanında getirmesini sağlamak güçlük çektiğimiz bir konu iken neredeyse yüzde yüz oranla yanlarında getirmeye başladılar. Onlar için araç gerecini getirmemek keyif aldıkları bir şeyden mahrum kalmak olacaktı sanırım. Evet, eğlenceli bir matematik oluyormuş. Ne teknoloji ne oyun ne de renkli kartonlar olmadan hem de.

Bahsettiğim Japon matematik dersindeki öğretmen öğrencilerden soru üretmelerini istediğinde şöyle bir cümle kuruyor: “Teslim ettiğinizde soruyu çözebilmelisiniz. Biri anlamadığını söylüyorsa, sorunun ne olduğunu ve neden olduğunu söyleyebilmelisiniz.” Öğretmenin bu cümleleri, Matematik Öğretimi Topluluğu olarak çalışmamızın ikinci fazında incelediğimiz “İlkokul ve Ortaokul Matematiği: Gelişimsel Yaklaşımla Öğretim” adlı kitabında, John A. Van de Walle ve arkadaşlarının matematik yapmak tanımını getiriyor aklıma: “Matematik yapmak , bir problemi çözmek için yöntemler üretmek, bu yöntemleri uygulamak ve bulunan bir cevabın mantıklı olup olmadığını kontrol etmek anlamına gelir.”

Bizler teknolojisiz, oyunsuz etkili bir öğretim olmayacağını düşünürken nasıl oluyor da sadece bir cetvelle bir derste matematik yapıldığını hissediyoruz, düşünüyoruz?

“Japon öğretmenlerden görüp kendi dersimde uygulamaya çalıştığım şey ne kadar yapılandırılmış?”, “Daha iyi olabilir mi?”, “Nasıl daha iyi olabilir?” gibi çokça soru tartışılıp üzerinde düşünmeye açık elbette. Fakat bu deneyimden ulaştığım net bir sonuç var: aslolan öğrenmeye elçilik edecek her şeyi yerine göre ve gerektikçe kullanmak. Zengin öğrenme ortamları tasarlamak, öğretmenden öğrenciye tek yönlü bilgi akışı yapıp sonrasında, çoğu zaman “pekiştireç” olma düzeyinde kalan materyalleri, teknolojiyi, renkli kartonları vs. sınıfa getirmekten çok daha fazlası. Zengin bir öğrenme ortamı, bilgi ve beceriyi kazanma sürecinin sonucuna değil, beceriyi kazanmanın kendisine hizmet etmeli ve süreçte öğrenciyi de aktif kılmalı.

Bu yazı, Matematik Öğretimi Topluluğu üyelerinin hayata geçirdiği “Matematik Öğretmeninin Gözünden Yazı Dizisi” kapsamında yazılmıştır. Yazı dizisine dair bilgi almak için buraya tıklayın.